Why Early Tokens Matter, and How Tree-of-Thoughts Tries to Fix It

Recently, I’ve been reading papers on LLM reasoning. They all say the same thing: if you let the model “think” before answering, accuracy improves. But I still didn’t understand why such a tiny prompt change (“think step by step”) makes such a big difference, so I tried a small experiment myself.

Prompt matters (but why?)

Giving example on why prompting matters isn't especially hard. Here's a small arithmetic calculation that I gave to the non-thinking model (GPT-5 instant) (correct answer is 617).

And here's the same problem with small prompt change:

So what happened? Given the exactly same problem to the LLM, one forced to only give the answer, the second one also give the reasoning for it, and we see two different results. Why does the "think step by step" magically fixes the model? To understand that, we need to talk about how LLMs actually produce their first few tokens, and why these tokens are so "fragile".

Early Tokens Matter!

LLMs generate text one token at a time, from left to right. Once a token is produced, it can’t be “taken back”. Every new token must continue from whatever has already been written, even if the early tokens were wrong. In tasks where the model must output only one number, once the first digit is wrong, it cannot reach the right answer.

So in the example where the model outputs 5 as the first digit when the correct answer is 617, the model is already locked into a wrong trajectory. From that point on, it must try to continue the sequence starting from 5, and the correct path is no longer reachable.

But before producing the first token, the transformer has already performed a large amount of parallel computation over the entire prompt, building a rich internal representation of the problem. We can think of this as the model internalizing the context and the task before it writes anything to the user. This internal state (sometimes called the model’s hidden state or contextual representation) determines the probability distribution for the next token, e.g., which token is most likely to come next.

What's great about LLM is that this internal state is recomputed every time we do a forward pass (calculate the next token from the LLM). Each new token is appended to the sequence, and another forward pass is done over the recomputed sequence!

"Stabilizing" the Models Internal State

So what happened when we allowed the model to generate intermediate reasoning (chain-of-thought) before giving the answer? Well, the output became larger. This means that each new token the LLM outputs becomes additional context for the next forward pass. Like I said, when a new token is generated, the LLM recomputes its internal state.

These intermediate tokens act as stabilizing feedback for the model. The model can “see” the steps it has already written, recompute its internal state on every token, and adjust its future tokens, which often helps it avoid or correct earlier mistakes. But stabilization doesn't explain everything, we need more deeper ideas to reason with:

Explaining LLM Outputs as Trajectories

When I say model stabilizes itself, what does that really mean? Sometimes LLMs are very confident that their wrong answer is right, sometimes long answers drift to nonsense or sometimes models "lock in" to bad reasoning, never being able to recover back to correct "path".

So it is beneficial to create mental models on what happens internally when model generates tokens.

One way to think about this is to think that LLMs moves through a high-dimensional internal space!

Before generating the first token, your prompt "pushes" the model into some region on that high-dimensional space. This is the models initial internal state.

Then tokens gets generated. For each of them we recompute the internal state (do forward pass), which moves the model to another space in this huge space! So each token is basically generating new point in this high-dimensional space.

But if you connect these points together, token-by-token, you get something that's useful to think about: trajectory.

Some trajectories (token-by-token generations) lead to structured reasoning, some lead to shortcuts, some starts to hallucinate or guess. But certain regions of hidden-state space tend to lead to consistent continuation patterns. We can loosely think of these regions as basins of attractor, e.g. the answer that given the initial state and trajectory, the output tends to go closer to certain region (output). Once the model find one of these regions, it tends to stay there.

Here I have simplification of trajectories and basins.

And here comes the important part: prompting strategies such as Chain-of-Thought helps the model not because it makes it smarter, but rather it breaks the problem into smaller subproblems that are easier to solve and drifts the answer closer to the basin!

When model the model writes these intermediate steps, each intermediate token constrains the distribution of future tokens, reducing drift.

But here's also a catch! Stablizing the trajectory (finding the trajectory model thinks works) doesn't mean that it is the correct one! However, as the trajectory stabilizes, the model becomes more confident on its' answer, which can then be seen models as confident on their own wrong answers!

So how do we make sure we don't stabilize the wrong trajectories that gives us the wrong answer? Well, one approach that can be used to create multiple trajectories and take only the best. This is the basic idea of Tree-of-Thoughts:

Why Tree-of-Thought works

If we think of finding solution to the problem with trajectories and basins, then the initial prompt is the starting position at the space, and pass througs make up the trajectory. This also means that early tokens have disportionate amount of influence to the output, if at early in the prompt the trajectory drifts away from structured reasoning, the model can become confident on wrong answer!

So the idea to fix this is just to give model multiple different trajectories that it can explore! Even if some of the trajectories are going to shift from the correct answer, with this approach we are more likely to get to the correct answer at least in one trajectory.

What prompting techniques such as Chain-of-Though do is to try to make it easier for trajectory to not drift to wrong directions, the Tree-of-Thought allows to try also other trajectories. This avoid the biggest weakness of CoT, committing too early to wrong trajectory and stabilizing it.

So the problem becomes, how do we do this, this is where the Tree-of-Thought paper is needed:

Implementation

How ToT paper handles this, is by maintaining tree of "thoughts", where each thought is a own full own intermediate step that helps to solve the problem. So instead of trying to solve the problem in one-pass, we first generate intermediate step that solves part of it, and where we can continue on trying to solve other parts of the problem. Important thing here is that each thought needs to give progress on solving the original problem, something should be done in order to be closer to the final value.

So we can think of them as our trajectories, each thought is new trajectory. After we have processed all the thoughts, we either generate new thoughts or we have an answer.

The basic implementation is just a tree data structure for the LLM.

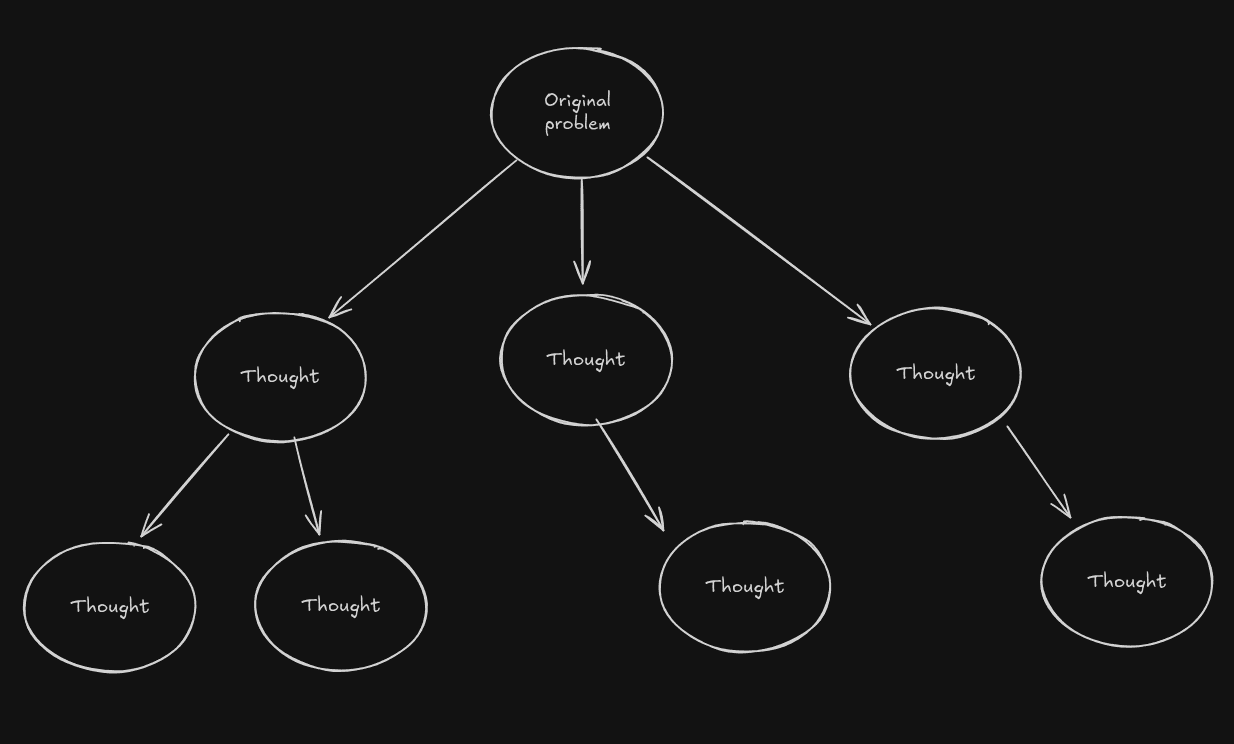
The paper frames the problem of finding the optimal solution to four different questions that need to be answered:

1. What the structure of the thought should look like?
2. How to generate thoughts from a state?
3. How to evaluate the state?
4. What tree search algorithm should be used?

Structure of the Thought

The first step for solving the problem, is to think what is the structure of our thoughts. Thought should be some intermediate step in the process of solving the problem, and should contain all the necessary information to keep solving the problem from the thought.

I'll use as example the Game of 24, which is simple game where given 5 numbers, you are asked how to obtain 24 from the numbers.

For example:

Numbers: [3, 3, 8, 1, 1]
Solution: (8 ÷ (3 − 1)) × 3 × 1 = 24

As an example ,this is very easy to understand what the structure of thought can be! Thought is just an list of numbers!

For example:

From each of these thoughts, we can try generate new thought by taking again two numbers and trying to solve the subproblem!

From Thought to State

Last example also shows how did we create the thought from a state, for the game of 24, it is just taking two numbers and generating new number from those.

But the problems we want to solve with ToT doesnt need to be this simple. The important thing is that each thought is progress on solving the problem, and we can easily go from thought to state. For example, creating itinerary for the trip, state could be the full itinerary, and thought could be single day in the trip. So the problem becomes generating multiple thoughts of single day, and adding those to itinerary attempts.

The paper and the code implementation uses two modes of thought generation:

1. Sampling “Give me k different continuations of this thought.”

Sampling here is just basically telling LLM to generate thoughts from the current state. This is especially good if ift's ahrd to generate all the possible states. E.g. in creative writing, we can't possibly write all the possible states, so we just have to generate some amount of them with sampling.

2. Propose: “List k possible next actions explicitly.”

Proposing is about giving the list of possible states that we can go next. For example in the game of 24, we actually have limited amount of ways we can calculate two numbers ( +, -, /, x), so we have limited set of states.

Here's also code from the implmentation, simple to understand, get_samples and get_proposals are just LLM calls to either get samples or list of proposals.

# generation
if args.method_generate == 'sample':
    new_ys = [get_samples(task, x, y, args.n_generate_sample, prompt_sample=args.prompt_sample, stop=task.stops[step]) for y in ys]
elif args.method_generate == 'propose':
    new_ys = [get_proposals(task, x, y) for y in ys]

Evaluation

We also need way to evaluate the thought we have processed. As each in each iteration we generate new thoughts from the current thought, the amount of thougts increases in expontential!

However, generating thought doesn't mean it is worth to keep processing all of them. We can take out thoughts that would not generate good output, if we have way to evaluate the thoughts! For example, in Game of 24, we can eliminate all the thoughts that we know for sure can't get to the number 24! E.g. numbers [1,2,3] can't get to the 24 in any way, thus we can just skip the tree branch from this node forward.

The ToT paper uses two ways to evaluate the thoughts: value and vote.

Value is just simply giving value of the how good the prompt (from 1 to 10), then just taking the thoughts have good valuation. Normally this way is used when there's some way to give value for the single thought, but might be hard for more open-ended questions.

For more open-ended questions, we can also use vote: ask the LLM to take N amount of thoughts that it deems to be the best. So instead of giving value, we just ask the LLM to give smaller set of the thoughts that are worth generating new thoughts from.

# evaluation
if args.method_evaluate == 'vote':
    values = get_votes(task, x, new_ys, args.n_evaluate_sample)
elif args.method_evaluate == 'value':
    values = get_values(task, x, new_ys, args.n_evaluate_sample)

Search algorithm

Finally, we also need to choose which search algorithm we want to use to search the tree we want to generate.

There are many different ways we can search the tree, and user should choose the best one that matches their goal, but the paper just used simple breadth-first search (BFS) and depth-first search (DFS). So basically, do we go tree in level order (BFS) or first maximally deepened in some dicrection and then backtrack to previous children (DFS).

But at what cost?

So we have the basic understanding of the implementation of the tree-of-thought, and how early tokens affect the output. What ToT does is that it gives us many different trajectories we can explore on, by giving the tracjectories in terms of new "thoughts".

As every thought is different from the other thoughts, we have different ways to approach the problem we are solving for. This then tries to stabilize at least one trajectory to the output space we are interested in by using smart evaluations at each thought-generating step. So the output will more likely get to the correct answer, as we are not limited to the single trajectory.

However, it comes with a cost. Each though that needs to processed needs it's own LLM call, then those thoughts are then used to generate new thoughts which also need it's own LLM call. The paper showed that it could give better performance than prompting strategies such as chain-of-thought, but it also used 100x more tokens to get to the answer! Even if the 1 ToT is better at giving the answer than 100 times doing CoT, it makes me wonder, is this really worth it, and how usable this would be in the real systems which more of often than not have limits on the time and the spending.

Tree-of-Thought prompting

However, the idea behind this can still be used! There's interesting way to use this idea of trajectories in a single prompt, and that is by in a single prompt itself try to give multiple "personas" that try to solve the same problem with different approaches.

There's good github repo on this type of prompting called Tree-of-Thought prompting. But the basic idea is to give the thoughts in single prompt, and let the model process those thoughts also in the single prompt. This of course means that we do not have the tree-search algorithm in the traditional sense, however, we have more appraoches to give the answer to the problem thatn just in traditional Chain-of-Thought. Let's give an example prompt:

However, how the output is given is highly related to the model, some propriety models such as Gpt-5 do not allow to show internal reasoning for the steps, so user can only see the output. And some models give quite large output to these problems. However, with this prompting technique, we can get a way for model to at least try couple more approaches to the problem, even if it is very limited compared to the full ToT.

Final "Thoughts"

Well, this blog was my attempt on explaining the importance of early tokens, using not so traditional concept of thinking the LLMs outputs as trajectories that stabilize to basin of attractors. Thinking of LLM reasoning as trajectories moving through a high-dimensional space isn’t literally how the math works, but it does explain a lot of what we observe every day:

• why the first token can collapse the outcome
• why long reasoning stabilizes answers
• why models can be confidently wrong
• why chain-of-thought works at all
• and why tree-of-thought helps escape bad early paths

Then I used these ides to explain Chain-of-Thought and Tree-of-Thought prompting techniques, which have shown actual perforamnce improvement when using correctly. However, something being more performant does not necessary mean it is better, as there are more than performance in most systems to care for, e.g. how much model should be better to justify 100 time more expensive / time consuming answer?

Still, understanding why these methods works makes them fell less "magical" and more as engineering tools. And for me, writing about it was the best way to get clear mental model in my own head.

Thanks for reading this far, and I hope my thoughts at least gave you new way to think why early tokens matter so much.