Teaching LLM to improve its own prompts
When working with LLM systems, the biggest bottleneck isn't writing the first prompt, but learning how to improve it. Real systems rarely rely on a single prompt or a single LLM call—they are chains of calls with many modules interacting with each other. Trying to improve them manually often feels like:
- editing one prompt accidentally broke another
- changing a single line now causes bugs in other parts of the system
- evaluating the performance of the system needs hundreds (or more) examples
- and all of this costs money!
This makes prompt engineering for real systems tedious, slow, and expensive.
At work, I’ve been able to optimize prompts in a more "machine-learning-driven" way using DSPy, a declarative framework for building modular AI systems that can automatically tune prompts for different components.
However, the way these optimizers actually work has always felt a bit mysterious. So I decided to dig deeper and build one of the best prompt optimization algorithms: GEPA.
This post is about what I learned while doing that:
- how prompt optimizers really work under the hood,
- how they “compile” better instructions automatically,
- and how surprisingly simple the core ideas become once you implement them yourself.
In this post, I’ll show how GEPA can automatically discover better prompts for multi-module AI systems, and what happens inside this optimization loop.
Generic Pareto (GEPA)
I chose to implement GEPA (Generic Pareto) because it is one of the popular prompt optimization algorithms available in DSPy. The original GEPA paper can be found here.
The paper itself is quite dense, so I'll break down the key algorithms and concepts in a more digestible format.
By looking at the GEPA algorithm from a high level, we can see that it consists of two main algorithms:
- Prompt Optimization Loop: This is the main loop that iteratively improves the prompts based on their performance.
- Candidate Selection: This algorithm selects the next candidate prompt to improve upon.
Main loop
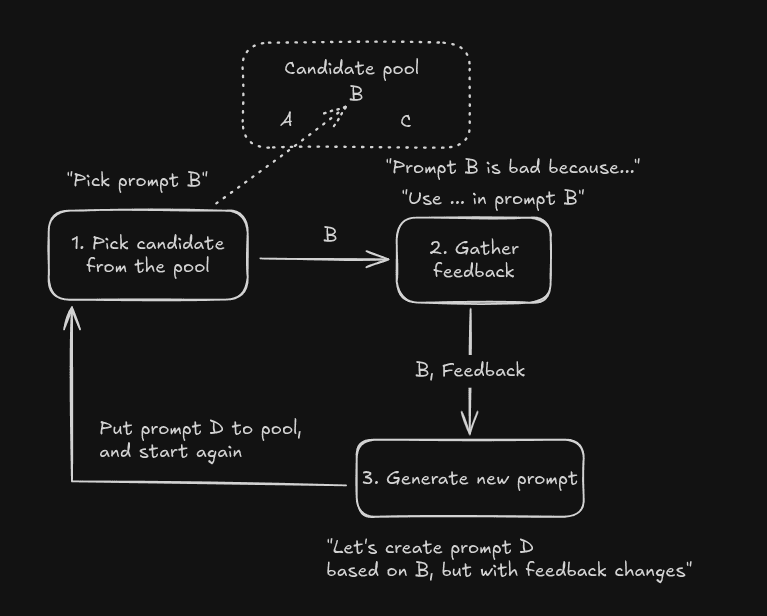
The basic idea is that we have a single main loop that we run each iteration. We gather a set of candidate prompts (initially just the base prompt), choose one of them to improve, generate feedback on how to improve the candidate prompt, and then create a new candidate prompt based on the feedback.

As you can see, the core of the algorithm is surprisingly simple:
- We have a list of candidate prompts, e.g. A, B, C.
- We select one of them, e.g. B.
- We generate feedback on how to improve B.
- We create a new candidate prompt D based on the feedback.
- We add D to the list of candidate prompts if it is better than prompt B.
This loop continues until we reach the maximum number of iterations we want to run.
Candidate selection
Another algorithm, and where GEPA gets its name, is the algorithm for choosing the next candidate prompt to improve. The name comes from the “Pareto front”. In simple terms, a Pareto front is just the set of prompts that are not clearly worse than any other prompt across all metrics. If one prompt is better in one metric but worse in another, both can stay. A prompt is only removed if there exists another prompt that is at least as good in every metric and strictly better in at least one.
How I understood that is: for prompts, we have multiple ways we can give "value" for the prompt. Some prompts are good in different metrics: one prompt might have the best precision, one the best accuracy, one might give the best performance in edge cases. So we have an optimization problem where we have more than one metric we want to optimize for.
So the Pareto front is just the set of these prompts where there is no other prompt that is best in all the metrics!
Let's give an example:
| Model | Quality (↑ better) | Cost (↓ better) | Pareto-Optimal? | Explanation |
|---|---|---|---|---|
| A | 70 | 1 | ✅ | No other model is better or equal in both quality and cost. |
| B | 80 | 2 | ✅ | Higher quality than A, slightly higher cost; not clearly worse than any. |
| C | 90 | 5 | ✅ | Best quality; although expensive, nothing is better in both metrics. |
| D | 85 | 5 | ❌ | Dominated by C (C has higher quality for same cost). |
| E | 60 | 4 | ❌ | Dominated by B (B has higher quality and lower cost). |
Pareto front = { A, B, C }
These are the options where you cannot improve one objective (quality or cost) without making the other worse.
So for GEPA, we want the list of prompts that are on the Pareto front, and then pick one of these prompts in each iteration.
And the final choosing of the prompt is also simple:
We give some single metric value (e.g. in the table example Quality * 0.5 + Cost * 0.5), based on the values, give the higher values bigger chance to be picked, and then just choose one randomly based on the chances! This way, better prompts have a better chance to be randomly picked, but we do not always take the best one because the prompt chosen is just by random luck!
Implementation
Now that we have the high-level understanding of how GEPA works, let's see how we can implement it from scratch.
What are we optimizing?
The original GEPA paper optimizes many different tasks, but for simplicity, I chose to optimize the HotpotQA task. HotpotQA is a question answering task where the model needs to answer questions based on given context paragraphs.
So I created a datatype to represent the example in HotpotQA:
class Example(BaseModel):
qid: str
question: str
context: List[Tuple[str, List[str]]]
gold_answer: Optional[str] = None
gold_supports: Optional[List[SupportRef]] = NoneWhere the question is the thing we want to find out, and the context is the list of paragraphs where the answer can be found. For simplicity, I also built the most simple multi-model DSPy module for the task:
import dspy
from .signatures import Reason, Verify
class HotpotModel(dspy.Module):
def __init__(self):
super().__init__()
self.reason = dspy.ChainOfThought(Reason)
self.verify = dspy.Predict(Verify)
def forward(self, question: str, context):
r = self.reason(question=question, context=context)
v = self.verify(question=question, context=context, rationale=r.rationale, candidate=r.candidate)
return { "rationale": r.rationale, "candidate": r.candidate, "answer": v.answer.strip() }The signatures are simple base prompts that we intend to optimize for:
class Reason(Signature := dspy.Signature):
"""From HotpotQA context, identify the bridge fact(s) and propose an answer.
Keep rationale to 2-4 lines. 'candidate' is a SHORT span."""
question = dspy.InputField()
context = dspy.InputField()
rationale = dspy.OutputField(desc="2-4 concise lines showing hops")
candidate = dspy.OutputField(desc="short answer span")
class Verify(Signature := dspy.Signature):
"""Verify or correct the candidate using the context and rationale.
Output ONLY the final short answer span."""
question = dspy.InputField()
context = dspy.InputField()
rationale = dspy.InputField()
candidate = dspy.InputField()
answer = dspy.OutputField(desc="short answer span")So the system is just one call to say the rationale for choosing the answer, and the second to verify. I could do the system with only the Reason call, but that way the algorithm would only try to optimize one prompt. For the sake of learning to optimize compound AI systems, I added the verify step so the task corresponds more to the compound AI systems.
Pareto-based candidate selection

Here's the actual algorithm used in the paper.
Here the P is the list of candidate prompts, and S is the list of scores for each prompt. So the first step is to find the best score for each example!
# Best score per example: s*[i] ← max_k S_P[k][i]
s = {}
for ex in D_pareto:
qid = ex.qid
s[qid] = max(
(S.get(k, {}).get(qid, {}).get("mu", 0.0) for k in P),
default=0.0
)I use scoring as that is calculated for each example. So now we have, for each example, the best prompts that achieve the highest score for the prompt. Notice that this can be multiple prompts if many prompts have the same highest score for the same example.
# Instance-wise winner sets: P*[i] ← {P[k]: S_P[k][i] = s*[i]}
P_star = {}
for ex in D_pareto:
qid = ex.qid
best_mu = s[qid]
winners = []
for k in P:
mu_k = S.get(k, {}).get(qid, {}).get("mu", 0.0)
if abs(mu_k - best_mu) < 1e-9:
winners.append(k)
P_star[qid] = winnersAfter getting the unique prompts from the list of all prompts that were the best for some example, we prune the "dominated" prompts. A prompt is dominated if, for all the examples, there exists a prompt which is at least as good, but at least for one prompt it is better. So basically if one prompt is always better than another prompt, we discard it!
# Prune dominated → P_optimal
P_optimal = prune_dominated(C, P_star)
if not P_optimal:
P_optimal = Cwhere
def build_winner_sets(P_star: dict[str, list[str]]) -> dict[str, set[str]]:
W: dict[str, set[str]] = {}
for qid, winners in P_star.items():
for k in winners:
W.setdefault(k, set()).add(qid)
return W
def dominates(a: str, b: str, W: dict[str, set[str]]) -> bool:
Wa = W.get(a, set())
Wb = W.get(b, set())
return (Wb.issubset(Wa)) and (Wa != Wb)
def prune_dominated(C: set[str], P_star: dict[str, list[str]]) -> set[str]:
W = build_winner_sets(P_star)
C_list = list(C)
D: set[str] = set()
for i, a in enumerate(C_list):
for b in C_list[i+1:]:
if dominates(a, b, W):
D.add(b)
elif dominates(b, a, W):
D.add(a)
return {c for c in C_list if c not in D}So basically, it is just creating "winner" sets and checking if one set is a subset of another. This works because in the last step we created the set of the best candidates. So if one set is a subset, it implies that both sets contain some same examples, and another set contains strictly more examples, meaning that the prompt corresponding to that set is better in all the examples.
Lastly, we create frequencies of the prompts (how many times it was best in examples):
P_hat_star = {
qid: [c for c in winners if c in P_optimal]
for qid, winners in P_star.items()
}
# f[Φ] = # of i with Φ ∈ P̂*[i]
from collections import Counter
freq = Counter()
for winners in P_hat_star.values():
freq.update(winners)
frequencies = {c: freq.get(c, 0) for c in P_optimal}and use that to pick one by random:
# Sample Φ_k ∝ f[Φ_k]
candidates = list(frequencies.keys())
weights = list(frequencies.values())
if sum(weights) == 0:
weights = [1] * len(candidates)
chosen = random.choices(candidates, weights=weights, k=1)[0]
return chosenThat's it! We just choose the best prompts on examples, filter out prompts that are worse than other prompts which gives us a list of best prompts in all examples. Then just pick one of those by giving the prompts weight and taking one randomly by the weights.
Main loop algorithm
Initialization

Now we get to the most important part: how to improve the LLM prompt.
I chose to use DSPy for this and create my own DSPy optimizer which works like GEPA (DSPy also has full GEPA already implemented, but I chose to build it from scratch).
DSPy optimizers are a class of Teleprompter, which needs one method compile, which takes the DSPy module (the program we want to optimize) and the training set.
from dspy.teleprompt.teleprompt import Teleprompter
# Main GEPA optimizer
class GEPA(Teleprompter):
def __init__(self):
super().__init__()
# Initialization here
def compile(self, student: dspy.Module, trainset: List[Example]):
# Logic hereThe algorithm splits the training set into two distinct sets: and
D_feedback, D_pareto = self._split_trainset(trainset, n_pareto)
The feedback set is used to gather feedback for the prompt, and the Pareto set is used to evaluate the performance of different prompts.
The first step is to get the base performance of the system we want to optimize for. This can then be used to compare if our new candidates are better than the original system:
# Get base performance
for ex in D_pareto:
out = student(question=ex.question, context=ex.context)
pred = out["answer"]
em = exact_match(pred, ex.gold_answer)
f1_ = f1(pred, ex.gold_answer)
mu = 0.7 * f1_ + 0.3 * em
S["base"][ex.qid] = {"em": em, "f1": f1_, "mu": mu}Then we need to get the information about the system we want to optimize for, for example, the module names and the list of initial candidates (prompts):
names = self.module_names(student)
candidate = self.snapshot_candidate(student)
candidates: Dict[str, Dict[str, str]] = {"base": candidate}While loop
If you look at the algorithm, we now have everything to start the main while loop in the algorithm.
For each iteration:
iteration = 0
while iteration < B:
# Logic here
iteration += 1we select the candidate (Pareto-based candidate selection), and the module we want to optimize (round-robin):
k = select_candidate(D_pareto, P, S)
current_candidate = candidates[k]
module = names[iteration % len(names)]Create a minibatch (small subset of ) to gather feedback from:
minibatch = random.sample(D_feedback, minibatch_size)
Then we create the new program containing our prompt and run that. After running and getting the output, we can give the feedback function the outputs that the model gave in our program:
for ex in minibatch:
output = instrumented_student(question=ex.question, context=ex.context)
# Gather all the info you want to send the feedback function:
# e.g. f1_metric = f1(output['answer'], ex.gold_answer)
fb = self.feedback(f1_metric, module_name, question, context) # Get the feedback, give it context of the last call
fb_content = {
"input": latest_inputs["inputs"],
"output": latest_inputs["outputs"],
"feedback": fb
}
feedbacks.append(fb_content)That's the basic loop for iteratively improving prompts with GEPA.